今回の講義：前回の宿題の答え

今回は前回の宿題の解答を題材に講義をしていきましょう。２次元座標空間における代表的な一次変換には次の４種類があり、これら以外の変換も全てこの４種類の組み合わせにより表せます。

  1. 回転
  2. 反転(折り返し)
  3. 拡大(縮小)
  4. 歪曲(斜交化)

歪曲だけは少し例外的で、組み合わせて一次変換の全パターンを網羅するために他の最初の３つに無理矢理付け足したようなものです[*1]。また、２次元→２次元以外の、２次元→ｎ次元（ｎ≠２、ｎ≧０）の変換はここでは考えていません。[*2]

一次変換とその行列

ここで思い出してほしいのですが、第一回で斜交座標の心であるベクトルの一次結合の話をしました。斜交座標変換つまり一次変換とは、図形的な意味としてはこの芯である定ベクトルを別のものにするという変換でした。ちなみに、この芯になるベクトルのことを基底もしくはベクトルであることを強調して基底ベクトルと呼びます。そして第二回では、その２つの定ベクトルの成分を並べて作った２次正方行列を掛けることで一次変換を表せることを解説しました。この考え方で４種類の一次変換を表す行列がどのようなものかをそれぞれ見ていきましょう。

１．回転

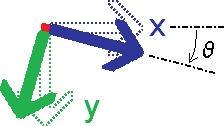
図１：θ回転での基底の変化を表した図

なでしこの座標ではＹ軸が下向きであることに注意してください。図は、原点中心・時計回りにθ回転させる一次変換における基底ベクトルの移り変わりを示したものです。Ｘ軸の基底ベクトルはθの方向の単位ベクトル(cosθ,sinθ)へ、Ｙ軸の基底ベクトルは(θ+π/2)の方向の単位ベクトル(cos(θ+π/2),sin(θ+π/2))＝(-sinθ,cosθ)へ移っています。つまり、この一次変換を表す変換行列Ａは、[[a11,a12],[a21,a22]]＝[[cosθ,-sinθ],[sinθ,cosθ]]となるわけですね。

図：θ回転行列Ａ＝[[cosθ,-sinθ],[sinθ,cosθ]]の行列表示

この行列は数Ｃの教科書にも載っているので、習って知っている人も多いでしょう。非常に使い勝手が良いので、是非覚えておいてください。[*3]

２．反転(折り返し)

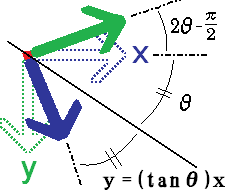
図２：直線y=(tanθ)xについて折り返したときの基底の変化を表した図

直線y=(tanθ)xについて折り返す変換（対称移動）も一次変換です。図は、２つの基底ベクトルを直線について折り返した様子を示したものです。Ｘ軸の基底ベクトルは2θの方向の単位ベクトル(cos2θ,sin2θ)へ、Ｙ軸の基底ベクトルは2θ-π/2の方向の単位ベクトル(cos(2θ-π/2),sin(2θ-π/2))＝(sin2θ,-cos2θ)へ移っています。つまり、この一次変換を表す変換行列Ａは、[[a11,a12],[a21,a22]]＝[[cos2θ,sin2θ],[sin2θ,-cos2θ]]です。

図：直線に関する対称移動を表す行列[[cos2θ,sin2θ],[sin2θ,-cos2θ]]の行列表示

これも高校数学で出てきますが、コラムや豆知識として出てきますね。覚えている人はこの行列も暗記しているかもしれませんが、暗記していなくても、基底の変化ということを理解しておけば、同じような図を書いて基底の成分を並べればすぐに行列を導き出せます。

３．拡大(縮小)

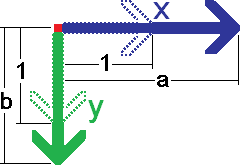
図３：ｘ軸をａ倍、ｙ軸をｂ倍に拡大したときの基底の変化を表した図

Ｘ軸方向をａ倍に、Ｙ軸方向をｂ倍に拡大(縮小)する変換も一次変換です。図は、それぞれの基底ベクトルをａ倍、ｂ倍した様子を示しています。Ｘ軸の基底ベクトルは同じ向きに長さａの(a,0)へ、Ｙ軸の基底ベクトルは同じ向きに長さｂの(0,b)へ移っています。変換行列Ａは、[[a,0],[0,b]]です。

図：Ｘ軸をａ倍、Ｙ軸をｂ倍に拡大する変換を表す行列[[a,0],[0,b]]の行列表示

これは一次変換としても行列としてもとても単純で分かりやすいのですが、それだけに重要です。この形の行列は対角線上にだけ成分があるので対角行列と呼び、高校数学でも、行列の対角化やべき乗の問題などでよく見ますね。また、例えばＸ軸の単位をセンチメートル[cm]からメートル[m]に換えるなどの単位・尺度の変換(スケール変換)とも考えられます。

４．歪曲(斜交化)

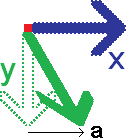
図４：ｙ軸をｘ軸方向にずらしたときの基底の変化を表した図

斜交座標変換が一次変換であることから明らかなように、直交座標を歪めるこの変換も一次変換です。図は、Ｘ軸の基底ベクトルをそのまま、Ｙ軸の基底ベクトルだけＸ軸方向にａずらして(a,1)に移した状態を示しています。変換行列Ａは、[[1,a],[0,1]]です。

図：ｙ軸をずらす変換を表す上三角行列[[1,a],[0,1]]の行列表示

左下の成分だけ０の行列を上三角行列と呼び、特にこの形の場合は対角成分が１なのでよく扱います。逆に、右上の成分が０の場合下三角行列と呼び、Ｘ軸をずらす変換を表す行列は下三角行列になります。対角行列ほど見ないかもしれませんが、やはりこれも高校数学で三角化やべき乗の問題で出てきます。

最初の３つの変換では、変換後の基底ベクトルが直交しており、座標系の直交性を保つ変換でしたが、４つ目に関しては文字通り座標系を歪めてしまいます。実用的な変換は最初の３つですが、この３つだけでは直交世界から抜け出せないため、歪んだ世界に飛び込むための変換が必要だったわけです。

前準備：行列グループをいつでも使えるようにする

さてそれでは実際に行列を使って上の４種類の一次変換を見ていこうと思いますが、その前準備として、前回扱った行列グループをいつでも取り込めるように、自分専用のライブラリとしてlibフォルダに保存する作業をしておきましょう。

matrix.nako
# 取り込み用ライブラリ：「行列」「ベクトル」グループ
■行列
　・{配列}要素
　・データ　←行列設定 →行列取得 デフォルト
　・行列設定(Ｖ)～
　　要素＝ＶをＣＳＶ取得
　・行列取得～
　　それは要素
　・掛ける({行列}Ｍを)～
　　Iとは整数。Jとは整数
　　ARRとは配列=M→要素
　　返り値とは配列
　　Iを0から(ARRの表行数-1)まで繰り返す
　　　Jを0から(要素の表列数-1)まで繰り返す
　　　　ARR[I]を反復、返り値[I][J]に対象*要素[回数-1][J]を直接足す。
　　返り値を戻す
■ベクトル +行列
　・一次変換({行列}Ｍで)～
　　要素=自身→掛ける(Ｍ)

これは前回のプログラム例で使用した行列とベクトルのグループの定義部分だけを取り出したものです。これを「matrix.nako」としてなでしこのライブラリフォルダ「nadesiko_lang\lib\」に保存すれば、いつでも取り込んで使えるようになります。nadesiko_langフォルダは通常、プログラムファイルズフォルダにインストールされているはずなので、フルパスだと「C:\Program Files\nadesiko_lang\lib\matrix.nako」になるでしょう。

これで準備終了です。あとは！『matrix.nako』を取り込むと書くだけでいつでも行列グループを利用できるようになります。それでは具体的に見ていきませう。

プログラム on Math

宿題の円は「(X-5)2+(Y-4)2=9」（中心(5,4)半径3の円）でした。これをそのままなでしこの座標系で描画しても小さく表示されてしまうので、３の拡大変換を利用して適当な大きさにして他の行列を組み合わせると分かりやすくなります。

回転して拡大する一次変換（宿題の解答例）
！『matrix.nako』を取り込む。＃１

uとはベクトル。vとはベクトル
θとは数値

Aとは行列。# 変換行列
Aは15度回転行列。
Bとは行列。# 拡大行列
Bは35倍拡大行列。

A=BをAに掛ける。＃２

u="8{~}4"
Aでuを一次変換
36回
　θ=回数*10をラジアン変換
　v="{3*COS(θ)+5}{~}{3*SIN(θ)+4}"
　Aでvを一次変換
　uからvへ線分を引く
　u=v

●線分を引く({グループ}uから{グループ}vへ)
　母艦のu→要素[0],u→要素[1]からv→要素[0],v→要素[1]へ線
＃３
●度回転行列({数値}DEG)
　θとは数値=DEGをラジアン変換
　Cとは数値=COS(θ)。Sとは数値=SIN(θ)
　「{C},{-S}{~}{S},{C}」を戻す
＃４
●反転行列({数値}DEGの)
　θとは数値=DEG*2をラジアン変換
　Cとは数値=COS(θ)。Sとは数値=SIN(θ)
　「{C},{S}{~}{S},{-C}」を戻す
＃５
●倍拡大行列({=?}A,B)
　もしAが空ならばA=B
　「{A},0{~}0,{B}」を戻す

プログラム解説

今回のプログラム自体はあっさりしていますが、解説で出てきた行列を組み合わせたり、第一回で使った座標軸も同時に表示させるなどして色々試してみるといいでしょう。

#1
前準備の所で用意したmatrix.nakoがそのままこのプログラムに取り込まれて使えるようにする。
#2
行列ＢＡにより引き起こされる一次変換は、Ａで一次変換をしたあとＢで一次変換するのと同じ変換。
#3
なでしこの座標系で原点中心に時計回りにDEG度だけ回転する変換の行列をＣＳＶ文字列で返す。
#4
なでしこの座標系で傾きDEG度の直線に関し対称移動する変換の行列をＣＳＶ文字列で返す。
#5
Ｘ軸方向にＡ倍、Ｙ軸方向にＢ倍に拡大する行列のＣＳＶ文字列を返す。Ａを省略するとＡ＝Ｂで補完され、単位行列ＥをＢ倍したもの[*4]になる。

まとめ

  • 代表的な一次変換は次の４種類
    1. 回転
    2. 反転
    3. 拡大
    4. 歪曲
  • 「一次変換の合成」＝「変換行列の積」と対応する

ちなみに全ての一次変換は上の４つの組み合わせで表せますが、その表し方は一意には定まりません。全ての行列も同様に、基本行列というものの積で表すこともできますが、やはり一意ではありません。

宿題

宿題の円「(X-5)2+(Y-4)2=9」に対してある一次変換を施すと、円形ではなくなる（正円でも楕円でもなくなる）。そのような一次変換を探し、またその必要条件を考察せよ。

次回からは行列式・不動直線・固有ベクトル・固有値などに関する話を扱っていきたいと思います。ここまでの数学的内容を理解できているならば、漠然とでもその条件はイメージできるはずです。

注釈

*1
実際には、その「歪曲」変換を表す行列が一番基本的な行列で、ほぼ全ての行列がこの歪曲変換を表す行列の積で表わされると言っても過言ではありません。しかし、図形的な意味で一次変換を分類した場合は、上の４つが代表的だということです。
*2
厳密に線形代数の言葉を用いて表現すると、一次変換ｆ：Ｕ→Ｖにおいて、dimＵ＝dim(f(Ｕ))＝２のときを考えている、ということです。dimＵはベクトル空間Ｕの次元（ディメンジョン）を表します。またf(Ｕ)はｆの像と呼び、Imｆとも表します。特に、dim(Imｆ)はrankｆとも表し、これを一次変換ｆの階数と呼びます。rankｆ＝１の一次変換は、高校数学でも行列の問題で出題されることがあるので、いずれ詳しく扱う予定です。
*3
回転を表す行列は、複素数のeiθ＝cosθ＋isinθ（i:=√-1は虚数単位）と同一視することができます。
*4
単位行列Ｅをスカラー倍（ｃ倍）したものを他の行列にかけると、各成分がｃ倍されるという性質から、この形の行列をスカラーと同一視して、簡単にｃとだけ記したりします。例えば行列の計算で、Ａ＋２Ｅを、Ａ＋２とだけ書いたりするのです。他にも恒等写像を１で表したり、∑記法で自明なインデクスを省くなど、数学ではよく簡単化された記法が採用されています。